La preparazione di un piatto particolare, una succulenta pietanza o anche di una tisana, richiedono spesso attenzione ai dettagli e il tempo, che spesso sembra non essere “mai abbastanza”, può essere un cattivo alleato se non lo si gestisce al meglio.
A chi non è capitato di servire una pietanza troppo calda, od ormai fredda, alla cena che da giorni stavi organizzando? A chi, in attesa di vedere il proprio programma preferito, non è capitato di andare al supermercato sperando di trovare una bibita già fresca, ma inevitabilmente disponibile solo nello scaffale non refrigerato?
Per cercare di prevenire ogni imbarazzo e soprattutto, avere bevande fresche a disposizione nei tempi stabiliti, proviamo a spiegare con alcuni esempi applicativi, il modello di scambio termico (trasferimento di calore) noto come legge di Newton del raffreddamento / riscaldamento (Newton’s law of cooling / heating).
T(t) = Ts + (To – Ts) e-kt
- t = tempo
- T(t) = temperatura del corpo al tempo t
- Ts = temperatura dell’ambiente (ad esempio la sala da pranzo, un frigo, una camera climatica)
- To = Temperatura iniziale del corpo (una zuppa, una braciola ai ferri, la lasagna della domenica 🙂 )
- k = costante
(raffreddamento con To > Ts , riscaldamento con To < Ts .
La formula, che in bibliografia si può trovare espressa anche in modi diversi, applicata con limitazioni di validità e nei trasferimenti di calore per moti convettivi e conduttivi, ci dice che, considerando maggiore è la differenza di Temperatura tra un corpo e l’ambiente nel quale si trova, piu’ rapidamente avverrà lo scambio di calore, il corpo perderà o acquisterà calore e più velocemente si raffredderà o riscalderà. Nella pratica, confermata dall’esperienza, un caffè caldo riposto in frigorifero, si raffredda più velocemente che a Temperatura ambiente.
Nel foglio di calcolo modello di Newton, sono riportate le soluzioni dei due esercizi che andiamo a riportare di seguito:
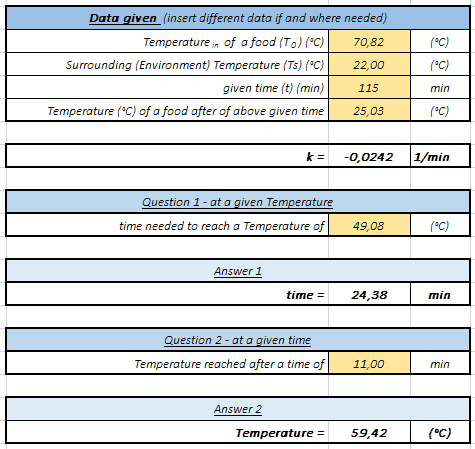
- “cooling_coffee“: supponiamo di avere appena preparato il nostro caffè pomeridiano partendo da acqua calda e caffè liofilizzato. La temperatura iniziale risulta essere pari a 70,82 °C. La Temperatura della stanza dove viene riposto il caffè, è pari a 22,0 °C (assumiamo che la Temperatura dell’ambiente si mantenga costante). Dopo 115 minuti (quasi 2 ore) la Temperatura del caffè’ risulta essere pari a 25,03 °C.
Dopo avere calcolato la costante k,
– stimare dopo quanto tempo il caffè risulta avere una Temperatura di 49,08 °C
– stimare la Temperatura raggiunta dal caffè dopo 11 minuti
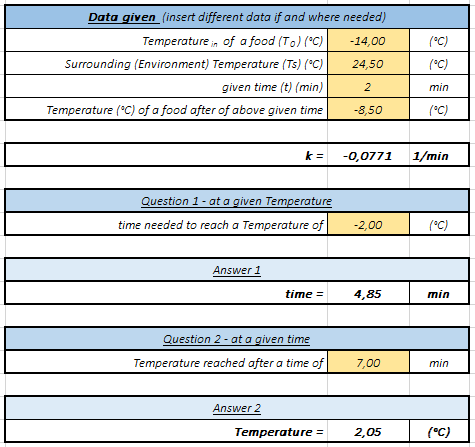
- “heating_icecream“: supponiamo di avere appena comprato un gelato presso la nostra gelateria preferita in una bella giornata di sole, con una Temperatura esterna di 24,5 °C (assumiamo che la Temperatura dell’ambiente si mantenga costante). Il gelato è servito ad una Temperatura di -11,5 °C e dopo 3 minuti arriva ad essere pari a -8,5 °C.
Dopo avere calcolato la costante k,
– stimare dopo quanto tempo il gelato risulta avere una Temperatura di -2 °C
– stimare la Temperatura raggiunta dal gelato dopo 7 minuti
Ci sono delle assunzioni alla base di tale modello, e non sempre lo stesso si dimostra puntuale nelle previsioni, in quanto diverse altre variabili entrano in gioco nel regolare gli scambi termici tra corpi e ambiente circostante. E’ un modello comunque valido per molte applicazioni quotidiane, soprattutto se il suo utilizzo è legato a valutazioni di screening o per ottimizzare i tempi in cucina.
Buon divertimento 😉 in attesa di verificare l’esattezza o la discrepanza dei valori predetti con un caso applicativo reale.